From Category Theory for Programmers - Series 1

Lecture 2

• A function is "pure" if you can memoize it
• For example, getchar() is not pure
• Functions
• How can they be used as morphisms in a category?
• Is a special kind of relation
• Relation is subset of pairs of elements for two sets
• Take two sets, S1 and S2 then a relation is some subset of the cartesian product S1 ⨯ S2
• Doesn't have direction
• Can have both one-to-many and many-to-one mappings
• Function can't have same input map to multiple outputs
• For the above example with S1 and S2, given a function 𝑓 to map between the two, S1 is the "domain" and S2 is the "codomain"
• The mapping from the domain to the codomain gives the "image" (subset of codomain)
• Given a function 𝑓,𝑔 (in Haskell notation) for the same a,b
• 𝑓 :: a → b
• 𝑔 :: b → a
• If 𝑓 ∘ 𝑔 = id_b
• And 𝑔 ∘ 𝑓 = id_a
• Then the function is invertible
• Also called isomorphism, (same definition for any category)
• When isn't there an isomorphisms?
• When a function collapses a set aka multiple elements in a domain map to a single element in the codomain (many-to-one)
• Or image is a proper subset of the codomain, so elements in the codomain can't be mapped back to the domain
• Injective function: one-to-one mapping, no many-to-one mappings
• Surjective function: onto mapping, no elements in codomain not in image
• What are the injective and surjective equivalents in category theory?
• Have to define using morphisms (arrows)
• Sort of defined for objects in relation to all other objects
• Category theory definitions are
• Injective: monic, or monomorphism
• Surjective: epic, or epimorphorism
• Defined for any category, more general than the definitions for functions in set theory
• But note there are some higher level technical details that cause these not to be the same as the concepts in set theory
• Epimorphism
• Consider the morphism 𝑓: 𝖷 → 𝖸
• If for every other object 𝖹 (in the whole category) and every pair of parallel morphisms g1,g2:𝖸→𝖹 it is true that (g1 ∘ 𝑓 = g2 ∘ 𝑓) ⇒ (g1=g2), then 𝑓 is an epimorphism (epic)
• This is also known as "right-cancellative"
• Going back to set theory, this is saying 𝑓 maps something to every element in 𝖸, but reminder that "epimorphism" in category theory is not the same as "surjective" with sets
• Had a hard time grasping this until I found the following example
• 
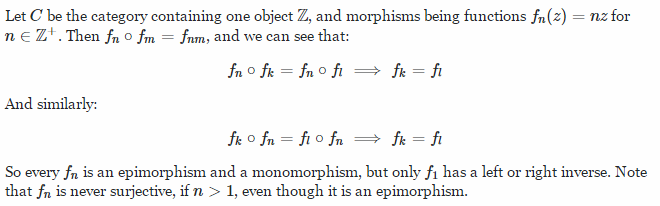
• https://math.stackexchange.com/a/81131/114910
• Monomorphism
• A non-injective function will map two different elements from one set to the same element in a different set
• Similar to epimorphism, but using precomposition instead
• Consider the morphism 𝑓: 𝖷 → 𝖸
• If for every other object 𝖹 (in the whole category) and every pair of parallel morphisms g1,g2:𝖹→𝖷 it is true that (𝑓 ∘ g1 = 𝑓 ∘ g2) ⇒ (g1=g2), then 𝑓 is a monomorphism (monic)
• This is also known as "left-cancellative"
• For epimorphism and monomorphism, the definitions depended on every object in the category
• Note: if an arrow is both an epimorphism and monomorphism, it doesn't mean it's isomorphic, like it would be in set theory
• Haskell and set theory
• Null set sort of corresponds to Void type
• No way to construct a Void
• f :: Void → Int
• That's a valid function, but can't be called because you can't produce a Void
• Actual has a name, the "absurd" function, and output can be any type (anything), not just Int
• Basic identity function is as follows
• idvoid :: Void → Void
• Next is one element set
• "Unit", empty tuple ( ), which has the same type ( )
• Gives "unit" function
• unit :: anything → ( )
• And lots of other functions that map unit to other objects, just returns a constant value
• So that allows referring to set elements with functions, which is based on the number of elements in the set. For example, Bool has two functions, one that returns true, one that returns false.