From Category Theory for Programmers - Series 1

Category Theory 5.1 - Coproducts, sum types

• Review of product
• Product in the opposite category is the co-product
• Two objects a,b with morphisms i,j into c
• 
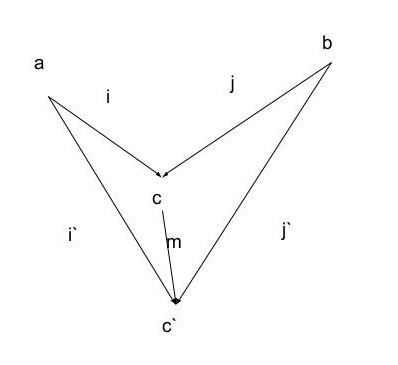
• Similar to product, but instead of saying the product is "The best" if there is a morphism to c, the condition is now morphism away from it, i`,j` into c`
• What is the coproduct in set theory?
• Embedding set a into c, and set b into c
• A maps into c, b maps into c, and nothing else
• Sort of union; ideally there is no overlap
• Discriminated union, which keeps information, such as element from left and element from right, even if mapping from same set
• Aka tagged union
• Aka variant
• Aka sum type
• Coproduct in haskell
• data Either a b = Left a | right b
• Can construct an element with type 'a' or type 'b'
• Category product had two functions 'fst' and 'snd' to extract either first or second argument
• coproduct has 'Left' and 'Right' to construct the object
• Can't immediately extract information for a given type (a) because it might have been constructed from the other type (b)
• "Pattern matching"
• Haskell example
• f :: Either Int Bool → Bool
• f (Left i) = i > 0
• f (Right b) = b
• Sum type in c++
• Say, a pointer to an object. Can be a null pointer, or it can be a pointer to valid data.

(part 2)

• Algebra of types
• In Haskell, looking at product
• Is a monoid product symmetric?
• Well, it doesn't have to be
• (a,b) is not the same as (b,a)
• But there is a swap function
• So the product is symmetric up to isomorphism
• Is it associative?
• Not necessarily
• ((a,b),c) is not the same as (a, (b,c))
• But can define an association function to rearrange
• Does it have unit?
• (a, ()) is not the same as a
• But is isomorphic
• Which means
• a ⨯ 1 = a
• In Haskell, looking at coproduct
• Symmetric?
• Either a b ~ Either b a
• Symmetric up to isomorphism
• Associative?
• Triple a b c = Left a | Right c | Middle b
• What's the unit of sum?
• Void
• Either a Void ~ a
• a + 0 = a
• What about a ⨯ 0
• a ⨯ 0 = 0
• (a, Void) ~ Void
• Can't construct an element of Void, so isomorphic
• Distributive?
• a ⨯ (b + c) = a ⨯ b + a ⨯ c
• (a, Either b c) ~ Either (a, b) (a, c)
• Have addition, multiplication, distribution, but not an inverse
• So not quite a ring
• Semi-ring
• 2 = 1 + 1
• Either () ()
• Say, call Left Unit true and Right Unit false
• Then this is the Bool type
• 1 + a
• Is "Maybe"
• data Maybe a = Nothing | Just a
• = Either () a
• Solving an equation
• L(x) = 1 + a ⨯ L(a)
• L(a) - a ⨯ L(a) = 1
• L(a) (1 - a) = 1
• L(a) = 1 / (1 - a)
• data List a = Nil | Cons a (List a)
• Can expand out the recursive definition
• L(a) = 1 + a + a⨯a + a⨯a⨯a + a⨯a⨯a⨯a ...