From Category Theory for Programmers - Series 1

Category Theory 8.1 Category Theory 8.1 - Function objects, exponentials

• Function types
• So far (in this series) functions are separate from types
• In set, functions between 'a' and 'b' form a hom-set
• So this hom-set is an object and can be treated like an object in a category
• Though in other categories this isn't always true
• That is, the set of morphisms is contained in set, maybe external to the category
• In set, a generalized description of functions and input and output is given by the cartesian product of the function object, the input object, and an arrow to the output object
• Function object 'z', input object 'a', output object 'b'
• z ⨯ a → b
• Which means the product must be defined
• If the category doesn't have products then there can't be a definition for functions
• Use universal construction to define the best description for a function
• Product is a bifunctor (takes two objects and produces a third), but also takes two morphisms and produces a third morphism (the product of these two morphisms)
• Needed to establish theory of products before showing the best description of a function
• For morphism g, from z ⨯ a to b
• And morphism g`, from z` ⨯ a to b
• z is better than z` if there is a morphism h from z` to z
• That means there's a morphism h ⨯ id between z` ⨯ a and z ⨯ a
• 
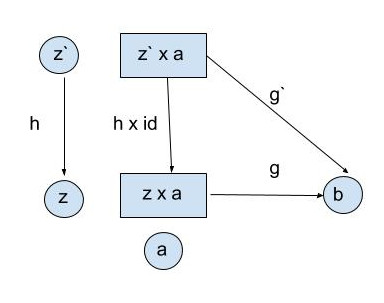
• g` = g ∘ (h ⨯ id)
• Part of the definition is that for every h there is a unique g`, so you can get one from the other
• g` is a function of two arguments, but h is only a function with one argument
• This is currying

h :: z -> (a -> b)
-- | which is the same as
g :: (z,a) -> b
curry :: ((a,b) -> c) -> (a -> (b -> c))
curry f = λ a -> (λ b -> f(a,b))
-- | corresponding uncurry
uncurry :: (a -> (b -> c) -> ((a,b) -> c)
-- | (f a) returns a function, which then calls b
uncurry f = λ(a,b) -> (f a) b

• In category theory this isn't called a function object, it's called an exponential
• This is written
• b^a
• Means the same as 'a' is the argument, 'b' is the return type
• a → b
• Given that functions are cartesian products, it's the number of possible pairs
• Bool -> Int
• Int^Bool
• Two values for Bool, say, 0,1
• Cartesian closed category (CCC):
• Has products
• For every pair of objects a,b, it has an exponential a^b
• Also has terminal object
• Bi-cartesian closed category also has coproduct
• Useful in programming
• Terminal object is kind of like zero'th power of an exponential

(part 2 - Category Theory 8.2 - Type algebra, Curry-Howard-Lambek isomorphism)

• What is a^{b + c}
• a^b ⨯ a^c
• Either b c -> a
• (b -> a, c -> a)
• (a ^ b) ^ c = a^{b ⨯ c}
• c -> (b -> a) ~ (b,c) -> a
• currying
• (a ⨯ b)^c = a^c ⨯ b^c
• c -> (a,b) ~ (c -> a, c -> b)
• So, this is extending algebraic data types to talk about functions
• Propositions in logic correspond to types in Haskell
• An inhabited type is true, uninhabited is false
• True is the Unit
• False is Void
• And: is a pair, can only form a pair with both types
• Or: Either a b
• Function type corresponds to implication
• Proposition: a ⇒ b
• Haskell: a → b
• Then this is extended to categories (cartesian closed category)
• Curry-Howard-Lambek isomorphism
• True is terminal object
• False is initial object
• And: is a product
• Or: coproduct
• Implication is exponent