From Category Theory for Programmers - Series 1

Category Theory 9.1 - Natural transformations

• Natural transformations are defined as mapping between functors
• Needs to preserve structure, the same way functors preserve structure
• A functor maps objects between categories
• Natural transformation is a way of picking a morphism from a hom-set (for every object)
• Things that make up the natural transformation are called "components" (the morphisms between objects)
• "Components" are the morphisms between objects in the second category
• Might be called vertical composition (see diagram)
• Natural transformation doesn't necessarily exist, but if it does, that means there's a relationship between the two functors
• 
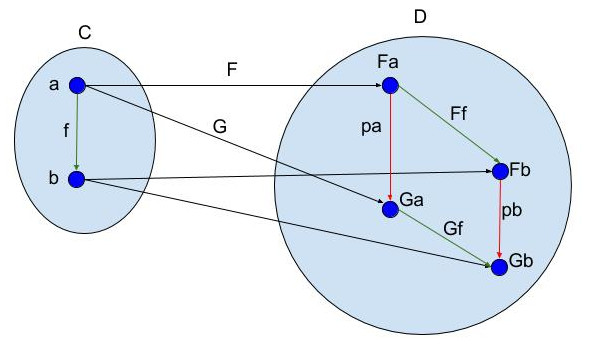
• "Naturality condition"
• Naturality square diagram (above)
• pb ∘ Ff = Gf ∘ pa
• Here 'p' are components
• (note: replaced 'α' with 'p' for readability)
• Natural transformation maps morphisms to commuting diagrams
• Some natural transformations are invertible, but not all are
• Invertible natural transformation is a "natural isomorphism"
• In programming, a natural transformation is a polymorphic function
• alpha :: forall a . F a → G a
• Parametric polymorphism, same formula for all types, which is much stronger than category definition
• Example, list functor and maybe functor

 
-- | head is a function that takes a list and returns the first element
-- | safe head to check for empty list
safeHead :: [a] -> Maybe a
safeHead [] = Nothing
safeHead (x : xs) = Just x
-- | parametrically polymorphic, same function for all types
-- | alphab ∘ fmapF f = fmapG g ∘ alphaa

• Natural transformation is a way of re-packaging containers
• Are all polymorphic functions natural transformations?
• A lot of them are
• In general, mapping between algebraic data types (including Identity and Const) is a natural transformation
• But not every polymorphic function is
• Contravariant functions

(part 2)

• Natural transformations are mapping of functors
• Do these mappings compose?
• Natural transformations α,β between functors F → G and G → H
• But the components are morphisms in the second category with arrows between them
• Via diagram chasing, it can be shown it composes
• It has an identity
• So functors between two categories form a category
• Functors are the objects
• Natural transformations are the morphisms
• Notation for functor category between categories C,D is [C, D] or D^C
• In cat, there are morphisms between categories (functors) and morphisms between functors (natural transformations)
• Functor morphism might be referred to as one cell
• Natural transformation morphism as two cell
• Zero cell for objects
• This is called a 2-category
• Locally small category means hom-sets are sets
• Hom-set in cat are morphisms between categories, but also it's own category
• So, cat is also cartesian closed
• Can we build a category instead of hom-sets has hom-objects?
• Well, yes, it's called an enriched category
• Horizontal and vertical composition
• Interchange law says one before the other is the same as one after the other
• Required for a 2 category
• Taking definition of 2 category and applying it up to isomorphism
• There is an associator morphism
• There is left and right unitor (left and right "identity")
• This is a bicategory