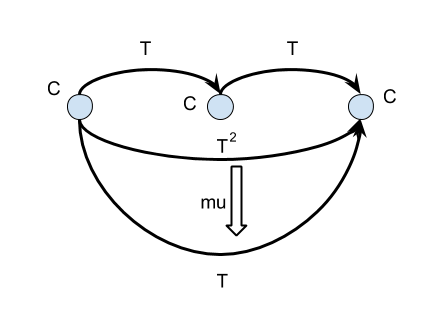
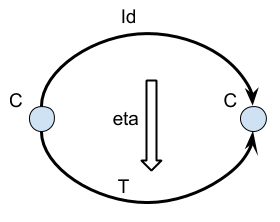
- Id → T
- T ∘ T → T
- Where arrow is natural transformation
- And, some additional requirements
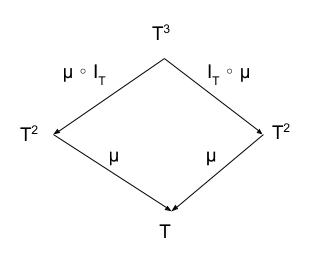
- Associative (for identity I)
- μ ∙ (μ ∘ I) = μ ∙ (I ∘ μ)
-
-
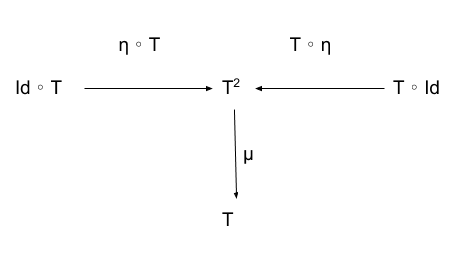
From Category Theory for Programmers - Series 1
Category Theory 10.1 - Monads
(>=>) :: (a -> m b) -> (b -> m c) -> (a -> m c)
-- | m is the embellishment
-- | m is a functor
-- | function f is a -> mb (these are types)
-- | function g is b -> mc
f >=> g = λ a -> let m_b = f a
in ...
-- | looking for a function like the following
:: m b -> (b -> m c) -> m c
-- | call it "bind"
(>>=) :: m b -> (b -> m c) -> m c
-- | then
f >=> g = λ a -> let m_b = f a
in m_b >>= g
-- | Monad definition is
class Monad m where
(>>=) :: m a -> (a -> m b) -> m b
return :: a -> m a
-- | what can be used from the fact m is a functor (in bind)?
-- | need another function
join :: m (m a) -> m a
-- | then, where f is (a -> m b) from (>>=)
m_a >>= f = join (fmap f m_a)
class Functor m => Monad m where
join :: m(m a) -> m a
return :: a -> m a
-- | join is actually provided by the Haskell library
-- | partial function a -> b -- | rewritten a -> Maybe b join :: Maybe (Maybe a) -> Maybe a join (Just (Just a)) = Just a -- | anything else, return nothing join _ = Nothing -- | alternative using bind -- | where f is a -> Maybe b Nothing >>= f = Nothing Just a >>= f = f a return a = Just a -- | another example -- | a function that depends on external state s a -> b -- | change to pass state with function (a, s) -> (b, s) -- | change to use currying a -> (s -> (b, s)) newtype State s a = State (s -> (a, s))




(part 2: 10.2 - Monoid in the category of endofunctors)
μ :: (a, a) -> a -- | set has element 'e' which is identity η :: ( ) -> a